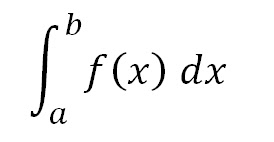Apartado II: La integral definida

La integral definida es una operación que tiene como principal aplicación el CÁLCULO DE ÁREAS Y VOLÚMENES en el plano cartesiano. Para representar matemáticamente una integral, debemos escribir lo siguiente:

Donde a y b son los límites de integración, f(x) es la función, y dx, diferencial de x.

En esta entrada, sólo pondré algunos ejemplos de integrales definidas de algunas funciones.

Ejemplo I: Cálculo del área gráfica y numericamente de la función x² entre los puntos de abcisas x=1 y x=2, con y=0.


Imaginad que nos queremos hacer una idea de cómo es dicho área. Al dar valores a x², se obtiene la siguiente función:

Bien, ya tenemos la función. Ahora nos queda determinar el área. Al no poner unidades, lo podemos dejar como unidades cuadradas (u²).



El ejercicio nos dice que el área a encontrar se encuentra entre x=1 y x=2. Lo señalamos.








La porción de plano cartesiano coloreada en rojo corresponde al área que queremos hallar. Este es el área, "resuelto" gráficamente.

-Ahora vamos a hallar el valor numérico del área, usando una integral definida:

Gracias a la siguiente fórmula, he podido hallar esta integral:

Ejemplo II: Calcula el área encerrada en la función y= cos x desde x=-π/2 hasta x=π/2 de forma gráfica y numérica.

• Gráficamente.
  

Porción en rojo=Área a hallar

• Numéricamente.

Aquí os pido que tengáis en cuenta una cosa. Si ya habéis dado derivadas, ya sabéis que:


f(x)=sen x -----> f ' (x)= cos x


O si habéis dado primitivas:


"Primitiva de cos x= sen x".


---->No tenéis más que aplicar lo anterior:

Las integrales pertenecen al análisis matemático, y en 2º de bachillerato se empiezan a utilizar.


Si queréis que ponga algún otro ejemplo, me lo decís, aunque de momento, sólo realizo integrales definidas sencillas. Recordad que derivación e integración son procesos inversos. Os puedo dejar algún ejercicio para que practiquéis:

-Ejercicio I. Cálcula el área de la función y=√x entre x=1 y x=5.

-Ejercicio II. Plantea una integral definida para el siguiente área de esta función y resuélvela:



Por si no lo véis bien, el área está comprendida entre 0 y 1.
Pista: Es una función potencial. (Ver Apartado I: Funciones).

Hasta aquí todo lo que puedo deciros de integrales definidas.
Espero que os haya gustado :) A continuación, os dejo algunos vídeos relacionados con las integrales y los teoremas fundamentales del cálculo, aunque también vídeos de derivadas. ↓